(I)证明:如图所示,连接AC,交BD于点O,连接OE.
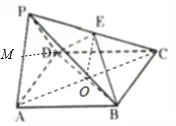
∵E为PC中点.∴OE∥AP.
∵AP⊄平面EBD;OE⊂平面EBD.
∴AP∥平面EBD.
(II)(i)当点M为线段PA的中点时,有DM⊥平面PAB.
下面先证明:AB⊥平面PAD.
∵四边形ABCD是平行四边形,∴AB∥CD.
又∵∠BAP=∠CDP=90°,即AB⊥AP,CD⊥DP,
∴AB⊥DP,DP⊂平面PAD,AP⊂平面PAD,
从而AB⊥平面PAD.∴AB⊥DM.
∵△PAD是正三角形,PM=MA,
∴DM⊥AP,
又AP∩AB=A,∴DM⊥平面PAB.
(ii)在(i)的条件下,点DN⊥PB时,有平面DMN⊥平面PBC.
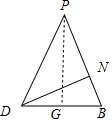
下面给出证明:在(i)的条件下,DM⊥平面PAB.∴DM⊥PB.
∴PB⊥平面DMN.
∴平面DMN⊥平面PBC.
不妨设AB=2,则PB=2

=DB,PD=2.取BD的中点G,连接PG.
则PG=

=

,
∴BN=DBcosB=2

=

.
∴

=

=

.
∴点N在线段PB的靠近点B的四等分点时,有平面DMN⊥平面PBC.



