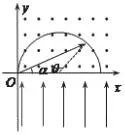
(1)粒子在磁场中做匀速圆周运动,根据洛仑兹力提供向心力:qvB=m$\frac{{v}^{2}}{R}$
可得粒子在磁场中运动的轨道半径:R=$\frac{mv}{qB}$
(2)粒子在磁场中运动的周期:T=$\frac{2πR}{v}$=$\frac{2πm}{qB}$,可知:t=$\frac{θ}{2π}•T$=$\frac{θm}{qB}$,
可得:θ=$\frac{qBt}{m}$
由图几何关系可知:s=2Rsin$\frac{θ}{2}$
粒子的位移随着时间变化的表达式:s=$\frac{2mv}{qB}$sin$\frac{qBt}{2m}$,其中t<$\frac{πm}{qB}$
(3)粒子在磁场中运动的周期:T=$\frac{2πm}{qB}$
根据牛顿第二定律可得:Eq=ma
故在电场中往返一次运动时间:t1=$\frac{2v}{a}$=$\frac{2mv}{qE}$
设第n次到x轴的位移为x,时间为t,平均速度为$\overline{v}$,
当n为奇数时,第n次到达x轴的位移:x=$\frac{n+1}{2}$•2R=$\frac{(n+1)mv}{qB}$,时间:t=$\frac{n+1}{2}$•$\frac{T}{2}$+$\frac{n-1}{2}$•t1=$\frac{(n+1)πm}{2qB}$+$\frac{(n-1)mv}{qE}$
平均速度为:$\overline{v}$=$\frac{x}{t}$=$\frac{2(n+1)Ev}{(n+1)πE+2(n-1)Bv}$
当n为偶数时:第n次到达x轴的位移:x=$\frac{n}{2}$•2R=$\frac{nmv}{qB}$,时间:t=$\frac{n}{2}$•$\frac{T}{2}$+$\frac{n}{2}$•t1=$\frac{nπm}{2qB}$+$\frac{nmv}{qE}$
平均速度为:$\overline{v}$=$\frac{x}{t}$=$\frac{2Ev}{πE+2Bv}$
答:(1)粒子在磁场中运动的轨道半径为$\frac{mv}{qB}$;
(2)粒子从出发开始计时,到第一次打到x轴前,粒子的位移随着时间变化的表达式为s=$\frac{2mv}{qB}$sin$\frac{qBt}{2m}$,其中t<$\frac{πm}{qB}$;
(3)粒子从出发到第n次到达x轴的平均速度的大小为$\frac{2(n+1)Ev}{(n+1)πE+2(n-1)Bv}$(n为奇数)或$\frac{2Ev}{πE+2Bv}$(n为偶数)。

